research
Exploring global features of networks using tools from topology, homotopy theory, algebra, and network science.
Higher-order Information Encoded in Networks and Point Clouds

My research deals with the analysis of higher-order information in networks and point clouds. A central motive is to use a blend of techniques from algebra, topology, and homotopy theory to explore the relationship between small scale connectivity data and other localised information, and large-scale behaviour and global properties of data sets.
Over the last years, availability of large, complex data sets has increased dramatically with recent advances in collection, storage and processing techniques. Extracting human-interpretable information from these is a challenging task across application scenarios. Standard methods of data analysis include projecting the data set onto subspaces with the highest variance (PCA), clustering the data points using closeness- or density-based clustering algorithms (k-means, spectral clustering, DBSCAN, etc.), or fitting polynomials or other functions to the data points. However in many cases, the information encoded in the point cloud cannot be retrieved by these methods: The detection of loops, voids, and holes in the point cloud requires tools that consider more than just proximity of points or local density. For example, these features are relevant when trying to analyse complex proteins consisting of multiple loops, or trying to understand the structure of a manifold in high-dimensional space from where the point cloud is sampled from.
From a different perspective, higher-order information are global features of the data-set. We cannot extract these from the local neighbourhood of a point of interest. However by combining all local information, higher-order global features arise. Because we are interested in information on the individual points, we finally need to find a way to localise these global features of the point cloud.
Combining Tools from Algebraic Topology and Network Science
Algebraic Topology is an area of Mathematics that was established trying to provide tools for capturing the “essence” of topological spaces. Topological features of a space are global and by design robust to local perturbations and noise, and are somewhat emergent properties of all the local connectivity data of the individual points. This is ideal for the setting of modern data analysis, where the goal is to extract information out of data sets where local perturbations are likely to occur because of noisy data collection.
Current tools of topological data analysis provide a good way of generating these global invariants (Betti numbers, persistence landscapes, etc.) from local connectivity data of point clouds. However, there is considerably less work on relating back these global features to the local scale of the points with a real-world meaning. This is surprising, considering that extracting information like cluster assignments on a point level is highly useful in application scenarios and a key goal of many areas of data analysis. Network Science, and especially signal processing on networks, on the other hand, deals with similar problems trying to connect the local connectivity information on network nodes to the global behaviour of the network and dynamics on it, and then relating this back to the individual nodes.
The overarching theme of my research is to combine perspectives of algebraic topology, network science, signal processing and clasical data anlysis to develop tools from extracting higher order information from point clouds and networks.
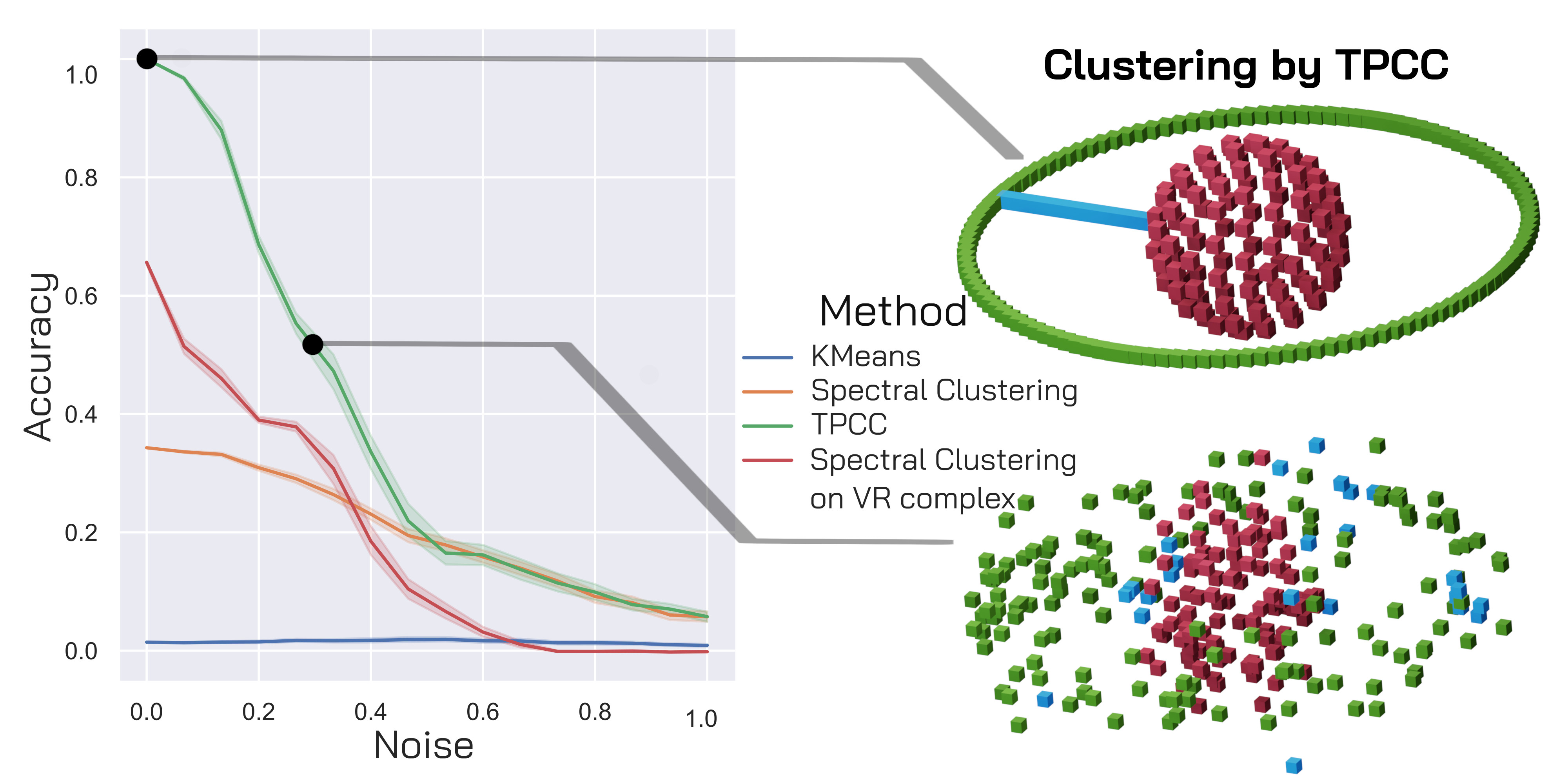
Project: Clustering Point Clouds in High-Dimensional Space Using Topological Information
Extracting information from a point cloud by clustering its points into different classes is one of most used concepts of data analysis. Standard clustering algorithms like \(k\)-means or Spectral Clustering, however, have a rather simple underlying notion of what makes different points belong to the same cluster: Proximity in space. However, sometimes correct cluster assignments can only be achieved using higher-order global information encoded in the point cloud. My research deals with trying to utilise various techniques from topology and algebra to generate meaningful topological features for clustering of point clouds. Topological Point Cloud Clustering (TPCC) uses a remarkable connection between the eigenvectors of Hodge Laplace operators of simplicial complexes and their topology to cluster the underlying points based on their topological roles.

For an up-to-date version of my research interests, please see the publications page.